Measures of nodes in a diffusion

These functions allow measurement of various features of a diffusion process:

• node_adoption_time(): Measures the number of time steps until nodes adopt/become infected

• node_thresholds(): Measures nodes' thresholds from the amount of exposure they had when they became infected

• node_infection_length(): Measures the average length nodes that become infected remain infected in a compartmental model with recovery

• node_exposure(): Measures how many exposures nodes have to a given mark

node_adoption_time(diff_model)

node_thresholds(diff_model, normalized = TRUE, lag = 1)

node_recovery(diff_model)

node_exposure(.data, mark, time = 0)

Arguments

diff_model

A valid network diffusion model, as created by as_diffusion() or play_diffusion().

normalized

Logical scalar, whether the centrality scores are normalized. Different denominators are used depending on whether the object is one-mode or two-mode, the type of centrality, and other arguments.

lag

The number of time steps back upon which the thresholds are inferred.

.data

An object of a manynet-consistent class:

• matrix (adjacency or incidence) from {base} R

• edgelist, a data frame from {base} R or tibble from {tibble}

• igraph, from the {igraph} package

• network, from the {network} package

• tbl_graph, from the {tidygraph} package

mark

A valid 'node_mark' object or logical vector (TRUE/FALSE) of length equal to the number of nodes in the network.

time

A time point until which infections/adoptions should be identified. By default time = 0.

Adoption time

node_adoption_time() measures the time units it took until each node became infected. Note that an adoption time of 0 indicates that this was a seed node.

Thresholds

node_thresholds() infers nodes' thresholds based on how much exposure they had when they were infected. This inference is of course imperfect, especially where there is a sudden increase in exposure, but it can be used heuristically. In a threshold model, nodes activate when \(\sum_{j:\text{active}} w_{ji} \geq \theta_i\), where \(w\) is some (potentially weighted) matrix, \(j\) are some already activated nodes, and \(theta\) is some pre-defined threshold value. Where a fractional threshold is used, the equation is \(\frac{\sum_{j:\text{active}} w_{ji}}{\sum_{j} w_{ji}} \geq \theta_i\). That is, \(theta\) is now a proportion, and works regardless of whether \(w\) is weighted or not.

Infection length

node_infection_length() measures the average length of time that nodes that become infected remain infected in a compartmental model with recovery. Infections that are not concluded by the end of the study period are calculated as infinite.

Exposure

node_exposure() calculates the number of infected/adopting nodes to which each susceptible node is exposed. It usually expects network data and an index or mark (TRUE/FALSE) vector of those nodes which are currently infected, but if a diff_model is supplied instead it will return nodes exposure at \(t = 0\).

References

On diffusion measures

Valente, Tom W. 1995. Network models of the diffusion of innovations (2nd ed.). Cresskill N.J.: Hampton Press.

See also

Other measures: measure_attributes, measure_central_between, measure_central_close, measure_central_degree, measure_central_eigen, measure_closure, measure_cohesion, measure_diffusion_infection, measure_diffusion_net, measure_features, measure_heterogeneity, measure_hierarchy, measure_holes, measure_periods, measure_properties, member_diffusion

Other diffusion: make_play, measure_diffusion_infection, measure_diffusion_net, member_diffusion

Examples

  smeg <- generate_smallworld(15, 0.025)
  smeg_diff <- play_diffusion(smeg, recovery = 0.2)
  plot(smeg_diff)

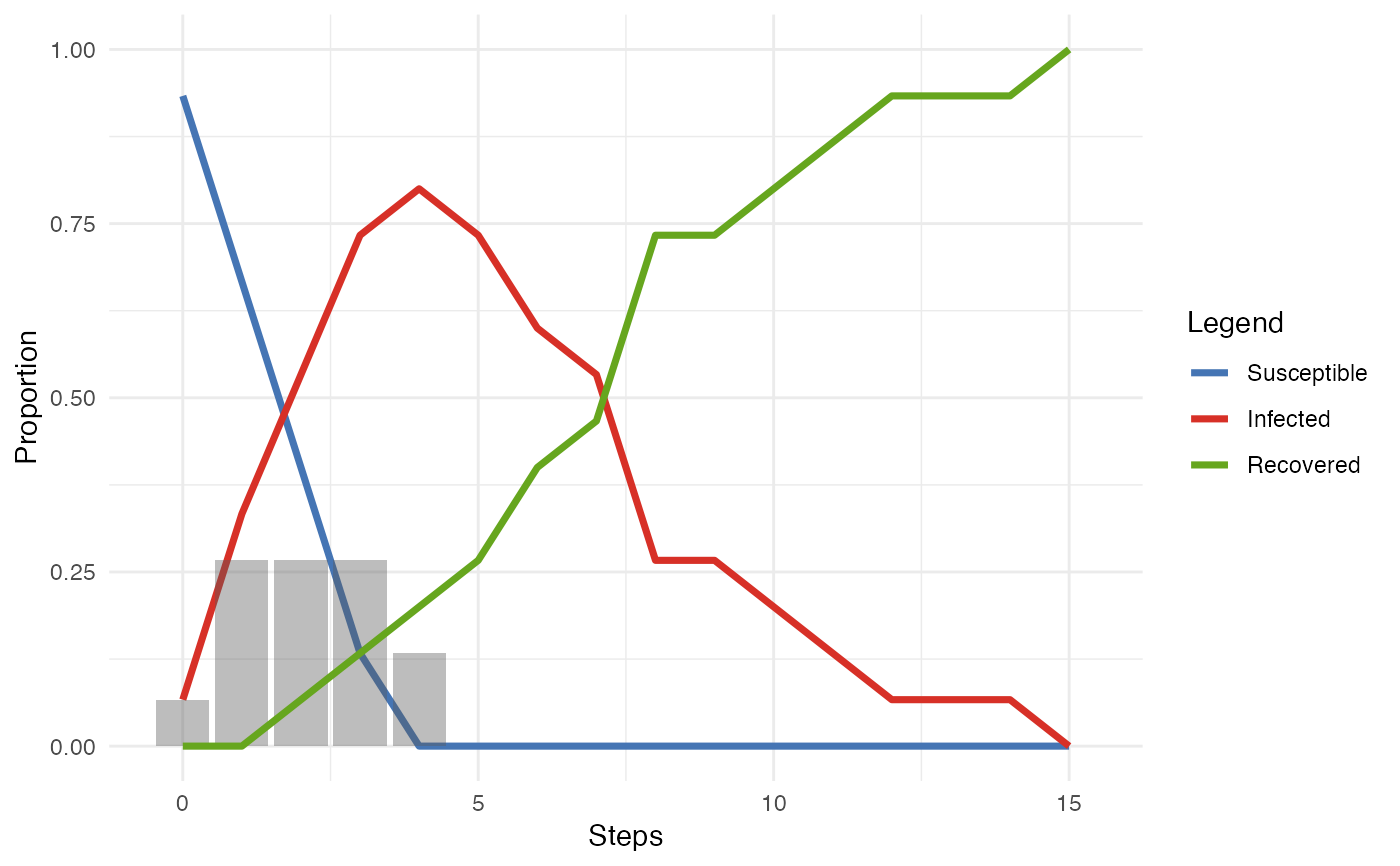  # To measure when nodes adopted a diffusion/were infected
  (times <- node_adoption_time(smeg_diff))
#>      V1    V2    V3    V4    V5    V6    V7    V8    V9   V10   V11   V12   V13
#> 1     0     1     1     2     2     3     3     4     4     3     3     2     2
#> # ... with 2 more values from this nodeset unprinted. Use `print(..., n = Inf)` to print all values.
  # To infer nodes' thresholds
  node_thresholds(smeg_diff)
#>     `1`   `2`   `3`  `14`  `15`   `4`   `5`  `12`  `13`   `6`   `7`  `10`  `11`
#> 1    NA  0.25  0.25  0.25  0.25   0.5  0.25  0.25  0.25   0.4  0.25  0.25 0.667
#> # ... with 2 more values from this nodeset unprinted. Use `print(..., n = Inf)` to print all values.
  # To measure how long each node remains infected for
  node_recovery(smeg_diff)
#>      V1    V2    V3    V4    V5    V6    V7    V8    V9   V10   V11   V12   V13
#> 1     6     2     3     6     6     5     5     3     8     7     2    13     9
#> # ... with 2 more values from this nodeset unprinted. Use `print(..., n = Inf)` to print all values.
  # To measure how much exposure nodes have to a given mark
  node_exposure(smeg, mark = c(1,3))
#>      V1    V2    V3    V4    V5    V6    V7    V8    V9   V10   V11   V12   V13
#> 1     0     2     0     1     1     0     0     0     0     0     0     0     0
#> # ... with 2 more values from this nodeset unprinted. Use `print(..., n = Inf)` to print all values.
  node_exposure(smeg_diff)
#>      V1    V2    V3    V4    V5    V6    V7    V8    V9   V10   V11   V12   V13
#> 1     0     1     1     0     0     0     0     0     0     0     0     0     0
#> # ... with 2 more values from this nodeset unprinted. Use `print(..., n = Inf)` to print all values.